Una de las primeras preguntas al iniciarse en Estadística es ¿Qué es el promedio? ¿Qué es la media aritmética? y, por consiguiente, ¿cómo sacar el promedio?
Que es la media aritmetica
La media aritmética es uno de los indicadores “estrella” en la estadística, ya que nos permite describir con un solo valor el comportamiento de una distribución de datos, aunque no lo haga de manera completa.
Como persona que se inicia en la estadística es necesario que sepas qué es la media en estadística.
¿Qué es la media en estadística?
A continuación, te explico todo lo relacionado con este estadístico descriptivo.
La media (promedio) de un conjunto de datos se encuentra al sumar todos los números en el conjunto de datos y luego al dividir entre el número de valores en el conjunto.
El término promedio se usa con frecuencia en la vida cotidiana para expresar una cantidad que es típica para un grupo de personas o cosas.
Por ejemplo, puede leer en un periódico que, en promedio, las personas miran 3 horas de televisión por día.
Por el uso del término promedio, entendemos que no todos miran 3 horas de televisión por día, pero que algunos miran más y otros menos.
Sin embargo, nos damos cuenta en el uso del término promedio que, la cifra de 3 horas por día es un buen indicador de la cantidad de televisión que se ve en general.
Los promedios son útiles porque resumen una gran cantidad de datos en un solo valor; e indican que, existe cierta variabilidad en torno a este valor único dentro de los datos originales.
La media es la medida matemática de promedio más utilizada (es decir, que hay otros tipos) y, generalmente, es a lo que se hace referencia cuando las personas usan el término promedio en el lenguaje cotidiano.
Cómo se calcula la media aritmética (cómo sacar promedio)
Aprender cómo sacar el promedio es relativamente fácil.
La media se calcula sumando todos los valores en un conjunto de datos; luego, este total se divide entre el número de valores que componen el conjunto de datos.
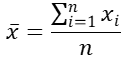
Por ejemplo, para averiguar el monto promedio recibido por 6 estudiantes de un grupo de tutoría que solicitó un préstamo estudiantil, se han recaudado los montos prestados a cada uno y se muestran en la siguiente tabla:
| Estudiante | Monto ($) |
| 1 | $ 650 |
| 2 | $ 800 |
| 3 | $ 500 |
| 4 | $ 450 |
| 5 | $ 900 |
| 6 | $ 830 |
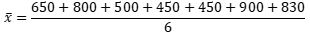
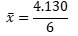
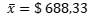
Se puede interpretar como: cada estudiante recibió un préstamo promedio de $ 688,33.
Cuándo usar la media aritmética
La media es una buena medida cuando un conjunto de datos contiene valores que se distribuyen de manera relativamente uniforme, sin valores excepcionalmente altos o bajos.
Es decir, la media se usa principalmente como un indicador general de datos, y funciona mejor cuando no hay muchos valores atípicos (1).
Cuándo no usar la media
La media es generalmente una medida inapropiada del promedio para los datos que se miden en escalas ordinales.
Los datos ordinales se clasifican según una categoría en la que un puntaje más alto indica un rango más alto o mejor que un puntaje más bajo.
Los datos ordinales se usan con frecuencia en encuestas que solicitan a las personas que indiquen preferencia (2).
La información final es relativa y la diferencia entre los rangos no es igual.
Por ejemplo, en respuesta a una pregunta sobre el sabor de una nueva mezcla de café, una puntuación de 10 implica un mejor sabor que una puntuación de 1, pero no significa que el sabor sea diez veces mejor (2).
No obstante, es aplicable en la evaluación de escalas semánticas con metodología Likert.
La media no se puede calcular con base en datos cualitativos.
Cómo analizar datos usando el promedio
El promedio es un término simple con varios significados.
En general, se refiere a una medida representativa del conjunto de datos, por lo que “esperamos” que la mayoría de los individuos presenten mediciones cercanas al promedio. Aquí aparece la noción de “esperanza matemática”.
Es necesario tener presente siempre que, el promedio es solo eso, un valor que recoge información y se puede interpretar como un punto de equilibrio del conjunto de datos.
Es por ello que siempre será importante considerar otras observaciones, como el valor mínimo y el valor máximo del conjunto de datos, con lo cual conoceremos el rango de los mismos, es decir, “desde cuánto” y “hasta cuánto” se distribuyen nuestros datos.
Usa la media para describir la muestra con un solo valor que represente el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de distribución de los datos.
Leer: Para qué sirve el Muestreo Estadístico
Ventajas de la media aritmética
- Funciona bien para listas que simplemente se combinan o se agregan juntas.
- Fácil de calcular: solo suma y divide.
- Es intuitivo: es el número “en el medio”, elevado por valores grandes y reducido por valores más pequeños.
- La media es útil para otros cálculos.
Desventajas del uso de la media aritmética
- La media es sensible a los valores extremos en los datos.
- El promedio puede ser sesgado por valores atípicos: no se maneja bien con muestras que varían enormemente. Por ejemplo, el promedio de 1000, 2000 y -3000 es 0, lo cual es engañoso.
- La media aritmética funciona muy bien el 80% del tiempo; se suman muchas cantidades y genera una convergencia aceptable. Desafortunadamente, siempre hay un 20% de situaciones en las que el promedio no encaja del todo (3).
Cómo sacar el promedio en Excel
Para sacar el promedio en Excel solo debemos aplicar la función PROMEDIO sobre el conjunto de datos, es decir, en el rango donde están ubicados los datos que queremos promediar.
Supongamos la siguiente serie de datos:
3, 8, 6, 2, 8, 5, 7, 4, 9, 8, 7, 6, 6, 7, 8
Los cuales están arreglados en las siguientes celdas:
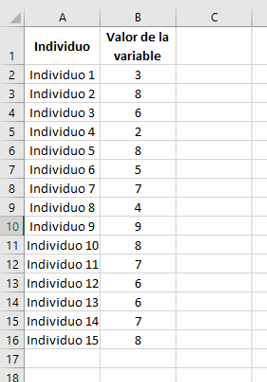
Ahora ubicamos la celda en la que queremos calcular y mostrar el promedio. Entonces, allí escribimos la fórmula:
=PROMEDIO(B2:B16)
Ya que los datos están distribuidos en la columna B, desde la celda B2 hasta la celda B16. Obteniendo el siguiente resultado:
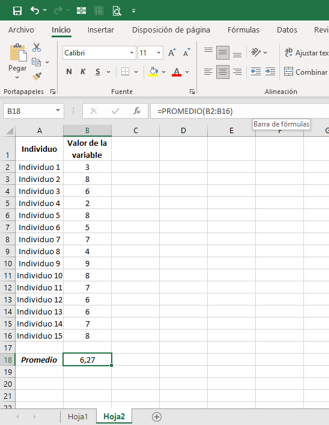
Ejemplo de Promedio en Excel
Conclusiones sobre cómo sacar el promedio
La media aritmética es un valor representativo y eficiente de un conjunto de datos cuantitativos.
El promedio es el centro de gravedad de los datos de una variable cuantitativa.
Se debe tener cierto cuidado al analizar datos con el promedio, ya que los valores atípicos generan sesgos o desviaciones fuertes sobre la media.
Finalmente, realizar el cálculo de la media en Excel es sumamente sencillo, basta con utilizar la función PROMEDIO y establecer el rango de los datos.
Referencias
- López, JF. 2022. Media aritmética. Disponible en: https://economipedia.com/definiciones/media-aritmetica.html
- Watson C. Difference Between the Mean & the Average. Sciencing.com. 2018. Disponible en: https://sciencing.com/difference-between-mean-average-6461324.html
- University of Leicester. Using averages. Student Learning Development. 2019. Disponible en: https://www2.le.ac.uk/offices/ld/resources/numerical-data/averages
Mira estos artículos disponibles
- 5 cosas que debemos cuidar en un ESTUDIO CUANTITATIVO
- El Paradigma Positivista en la Investigación Académica
- ¿Qué es la miología?
- Cómo funciona el Método Científico: Pasos Fundamentales de la Investigación
- Métodos de estudio: descubre los mejores métodos de estudio para potenciar tu aprendizaje
- ¿Qué es la investigación científica y por qué es importante?
- Ejemplo de la investigación de campo
- Temas de Tesis: cómo establecer un buen tema para la tesis
- Cómo escribir la dedicatoria y agradecimientos en la tesis
- Cómo evitar el plagio en los trabajos de investigación: técnicas y consejos
- Ficha Nemotécnica: Qué es, Tipos y Ejemplos
- La técnica de la encuesta: una herramienta esencial en la investigación cuantitativa













